高齢化だと、なぜ人手不足になるのか。「1人暮らし世帯増」というひとつの仮説

なぜ人口が減っているのに人手がこれほど不足するのか。この点について、先にまとめたレポート（「なぜ人口が減っているのに、労働需要が減らないのか」）において、統計から以下2点を指摘した。

国立社会保障・人口問題研究所が出した直近の世帯数推計（令和6(2024)年推計）では、2050年には単独世帯が44.3％に達し、また65歳以上の高齢世帯のピークは2045年とされる。高齢世帯増と1人暮らし世帯の増加は今後20年以上続く、日本社会のトレンドである。本稿では上記の①②の2点について、都道府県別パネルデータを構築し、各都道府県の人口動態や経済状況、労働市場の状況と組み合わせて分析することで、「高齢化がどのように人手不足を起こしているのか」という問題に一つの仮説を提示する。パネルデータの期間は2011～2019年である。

この期間に日本全体の65歳以上人口比率は23.3％から28.4％へと急速に伸長した。80歳以上人口比率は6.8％から9.1％へと増加している。こうした人口動態がどのような影響を与えたのかを分析する。

用いるデータの概要と仮説

分析に用いるデータは、以下の都道府県別統計（2011～2019年）である。

・県民経済計算（※1）　――GDP、産業別GDP、政府支出割合
・賃金構造基本統計調査（※2）　――労働者数、労働時間（一般労働者・短時間労働者）
・住民基本台帳（※3）　――年齢別人口動態、世帯数（※4）  
・統計でみる市区町村のすがた（※5）　――可住面積における人口密度
・自動車保有台数（※6）

構築した都道府県別の経年データをパネル分析することで、各都道府県の個別の状況を踏まえたうえで高齢化による労働市場等への影響を分析することができる。また、都道府県別GDPを都道府県別労働投入量（※7）で除することで都道府県別の1時間あたり労働生産性を算出することが可能である。

分析の基本的仮説は先般の分析結果を受け、以下のとおりとする。
◎80歳以上人口比率増加は、GDPの上昇、1時間あたり労働生産性の低下の影響を有する
◎世帯あたり人員数減少は、GDPの上昇、1時間あたり労働生産性の低下の影響を有する

GDPとの関係

まずはGDPへの影響について分析する。分析モデルは政府支出を除いた都道府県別GDPを従属変数とし、労働投入量、人口動態（80歳以上人口比率）、世帯あたり人員数等、上述の変数を独立変数として投入したものとなる。2011～2019年について分析する。

モデル1:モデル2:iは個体値（都道府県）、tは時点（年）である。YはGDP、α₁は独立変数X₁の回帰係数、α₂は独立変数X₂の回帰係数、X₁およびX₂は独立変数（80歳以上人口比率および1世帯あたり人員数）、βは統制変数Zの回帰係数、Zは統制変数（就業構造、人口密度等）、δは個体の固定効果、θ_i ＊trendは個体特有の傾向、ε_itは誤差項である。

このモデル（※8）における分析結果は以下のとおりであった。モデル１は主として80歳以上人口比率の影響を確認するもの、モデル２はモデル１の変数に加え1世帯あたり人員数を投入して影響を確認するものである。ほか、統制変数として各都道府県の経済社会の状況を反映すべく、変数を投じている。用いる変数については以下のとおり。

・政府支出除外GDP：従属変数。都道府県別の経済活動の推移を捕捉するため、その年の政府方針や大規模災害への対応など外在的な要素となる政府支出を除外している。
・80歳以上人口比率： 都道府県別の人口総数に占める80歳以上人口の比率。
・1世帯あたり人員数：都道府県別の1世帯あたり人員数。ライフスタイルの違いを示す変数として用いる。
・短時間労働者比率：労働投入量に占める短時間労働者の割合。各地域の労働市場や就業形態、働き方の違いを示す変数として用いる。
・生活維持サービス比率：都道府県別のGDPに占める生活維持サービス業種GDPの割合。ここでは生活維持サービスとして「建設業」「運輸業、郵便業」「卸売業、小売業」「医療、福祉」を抽出し、その産業別GDPの合計値の比率。各地域の産業構造の違いを示す変数として用いる。
・1人あたり政府支出額：都道府県別の政府支出額を人口で除したもの。各地域の産業構造・社会構造の違いを示す変数として用いる。
・1人あたり自動車台数：都道府県別の登録されている自動車台数を人口で除したもの。各地域の交通手段の違いや生活状況の違いを示す変数として用いる。
・人口密度（20％タイル、50％タイル、80％タイル）：市区町村別の人口を市区町村別可住面積で除し、同一の都道府県内の人口密度を昇順に並べた際の各分位点における人口密度。例えば20％タイル人口密度は、その都道府県における可住地域の人口密度が低い地点から20％に所在する地域の人口密度である。各地域の居住地の状況の違いを示す変数として用いる。

分析結果としては、80歳以上人口比率はモデル１においてはGDPに対して正に0.1%水準で有意な結果となった。しかし、1世帯あたり人員数を導入したモデル２においては、80歳以上人口比率の影響は有意でなくなった。他方で、1世帯あたり人員数はGDPに対して負に0.1%水準で有意である。1世帯あたり人員数が負に影響ということは、1世帯あたり人員数が高齢化によって減少していくことが、消費の稠密性を低下させ、人口あたりの消費額を押し上げ、結果としてモデル２のような世帯あたり人員数が減ることで需要（都道府県別のGDP）を増進させる影響が見られるという解釈ができる。

また、統制変数として投入している他の変数についてモデル２をベースに概説すれば、生活維持サービス比率は負に5%水準で有意である。その都道府県の産業構造において生活維持サービスの比率が高まると、GDPを押し下げる構造がある。20％タイル人口密度は正に5％水準で有意である。その都道府県における相対的な過疎地域の人口密度が高まると、GDPを押し上げる効果がある。

図表1　都道府県GDPに対する人口動態等の影響の分析（都道府県パネルデータの固定効果分析）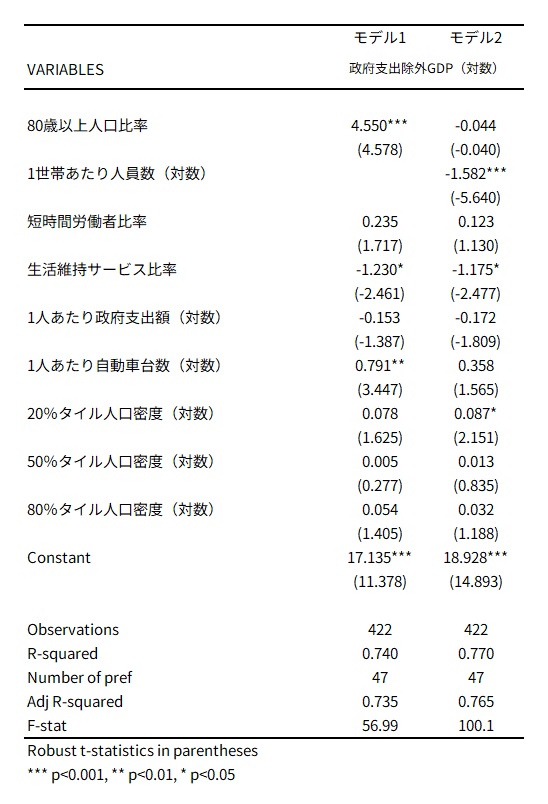
図表2　記述統計量（モデル上対数で投入しているものは実数値で表記）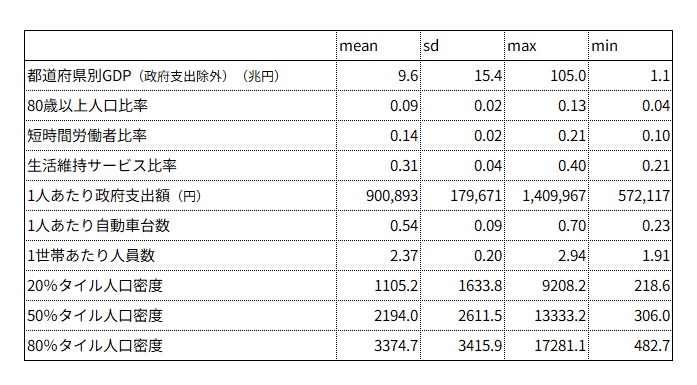

労働生産性との関係

次に、1時間あたり労働生産性への人口動態等の影響を検証する。分析モデルは政府支出を除いた都道府県別GDPを労働投入量で除した1時間あたり労働生産性を従属変数とし、人口動態（80歳以上人口比率）、世帯あたり人員数、経済規模（GDP）等を変数として投入したものとなる。2011～2019年について分析する。

都道府県別の経済規模を勘案すべく、先述のモデル1・2で用いた変数に加えて都道府県別GDPを統制変数として投入している。

モデル3:
モデル4:
iは個体値（都道府県）、tは時点（年）である。Yは1時間あたり生産性、α₁は独立変数X₁の回帰係数、α₂は独立変数X₂の回帰係数、X₁およびX₂は独立変数（80歳以上人口比率および1世帯あたり人員数）、βは統制変数Zの回帰係数、Zは統制変数（就業構造、人口密度等）、δは個体の固定効果、θ_i ＊trendは個体特有の傾向、ε_itは誤差項である。

分析結果は以下のとおりであった。80歳以上人口比率はモデル3においては、1時間あたり労働生産性に対して負に5％水準で有意である。80歳以上人口比率が上昇すると、1時間あたり労働生産性が押し下げられることを意味する。ただ、1世帯あたり人員数を投入したモデル4においては、80歳以上人口比率の影響が有意ではなくなり、1世帯あたり人員数が正に1％水準で有意であった。つまり、1世帯あたり人員数が増えると1時間あたり労働生産性が高まる（＝1世帯あたり人員数が減ると1時間あたり労働生産性が下がる）、という関係が存在している。

また、統制変数として投入した変数を概説すると、GDPは正に有意であり、経済規模が大きくなれば1時間あたり労働生産性が高まるのは、いわゆる規模の経済性とも解釈可能だが、モデルの特徴を踏まえれば景気循環要因に対して雇用量を調節しきれていないために好況期だと労働生産性が高まり、不況期だと労働生産性が低くなっていると解釈できる。生活維持サービス比率は負に有意であり、産業構造における生活維持サービス比率が高まると、労働集約的な産業であることもあり、1時間あたり労働生産性が低下する。1人あたり政府支出額は負に有意であり、政府支出が増えることで生産性は低下している。また、モデル4に関しては、1人あたり自動車台数は正に有意であり、自動車保有台数が増え行動範囲が広がることは経済活動の稠密性（商圏を広げられたり、医療施設を大規模化できたり）といったこととの関係が存在する可能性があるだろう。

図表3　1時間あたり労働生産性に対する人口動態等の影響（都道府県パネルデータの固定効果分析）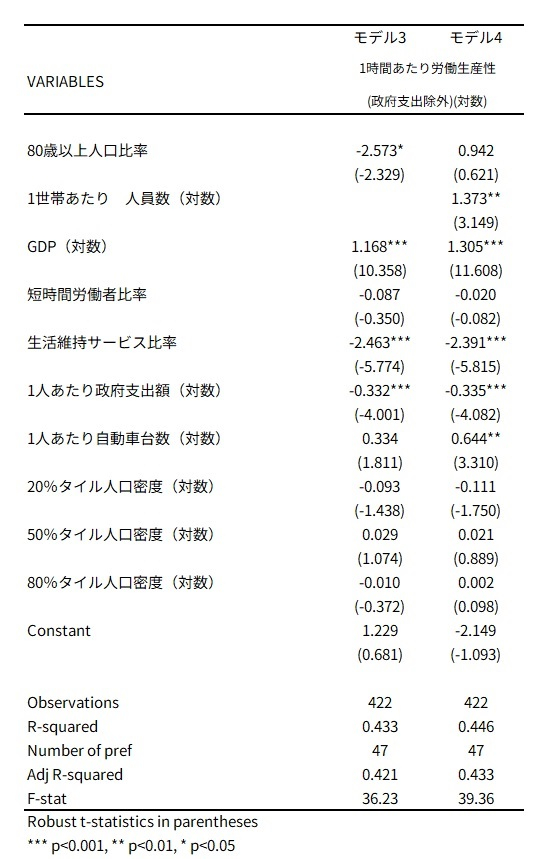

「1世帯あたり人員数」の減少も課題？

以上の分析結果をふまえれば、当初仮説は半分妥当で、もう半分は妥当ではなかったと判断できる。
すなわち、以下の結論が得られた。
◎80歳以上人口比率増加は、GDPの上昇、1時間あたり労働生産性の低下の影響を持たない
◎世帯あたり人員数減少は、GDPの上昇、1時間あたり労働生産性の低下の影響を有する

80歳以上人口比率の増加自体のみが課題ではなく、世帯あたり人員数が減少することで、需要が増加し、生産性が低下する。この結果として、目下の著しい労働供給制約（景況感と乖離した構造的な人手不足）が生じている可能性が示唆される。

このことは、高齢化社会においても、1世帯あたり人員数を維持することで、深刻な働き手不足を回避し持続可能な社会を構築できる可能性があることを同時に示唆している。この1世帯あたり人員数の維持とは、居住環境の稠密性を維持することと換言できる可能性もあり（無論、さらなる検証が必要だが）、単に「一緒に住む家族を増やす」ことだけでなく、

等々といった、居住空間の工夫によって働き手と労働の消費者の双方が豊かになれる可能性を内包している。またそれは、結果として大きな社会問題となりつつある「孤立」「社会的孤立」に対応することにもなるかもしれない。

ただ、1世帯あたり人員数が問題としても、1世帯あたり人員数の減少は80歳以上人口比率の影響を極めて強く受けている（※9）。また、80歳以上人口比率は生活維持サービス比率の増加へも強い影響を与えている（※10）。そしてその結果、1時間あたり労働生産性が低下しているのだ。

以上をパス解析的に概念図化したものが図表４である。都道府県パネルへの単回帰分析における有意水準を付している。75歳以上人口は2055年まで増加を続ける（※11）とされ、75歳、80歳以上の人口割合が減少に転じるのは、少なくともこの先30年以上難しいことは間違いがない。ただ、それに伴う深刻な働き手不足、生活維持サービスの水準の切り下げといった社会問題に対しては、1世帯あたり人員数の減少に対応する施策を打つことが有効である可能性があると言えよう。

図表4　「労働供給制約」が起こる理由の概念図（※12）

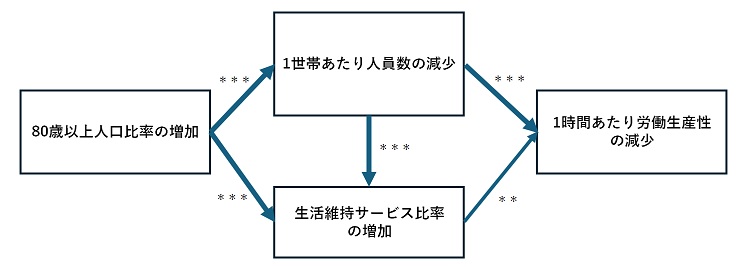
***:0.1%水準　**:1%水準