
労働需給シミュレーションの解説
はじめに
リクルートワークス研究所が2022年度に実施した「Works未来予測20XX」プロジェクトでは、日本の労働社会が近い将来直面する課題として「労働供給制約」に焦点を当てた。労働供給が速いスピードで減少し、「生活維持サービス」にも影響が及んでしまう状況に対して我々は何ができるのかを考え、解決策を提示している。
こうした未来の「はたらく」の姿を検討するとき、労働需給シミュレーション(以降、シミュレーションと表記)は検討の出発点となる。未来を「座して待つ」と労働社会はどうなるのか。何らかの打ち手を講じたとき、労働供給制約をどこまで解消できるのか。それらの姿を、経済、制度、人口などのマクロ統計、そして企業や団体など有識者の声から予測した。
本稿では、そのシミュレーションの構造や考え方について解説した。適宜、予測に用いた数式を掲載しているので、ご関心に応じてご参照いただきたい。
シミュレーションの流れ
リクルートワークス研究所が今回構築したシミュレーションモデルは、労働政策研究・研修機構 (2019) による『労働力需給の推計ー労働力需給モデル(2018年度版)による将来推計ー』の方法を参考にしている。シミュレーションは大きく、「需要ブロック」「供給ブロック」「需給調整ブロック」という 3 つのブロックで構成されている。
シミュレーションの手順を簡単に示すと、以下 2 つとなる。
1、上記 3 つのブロックに対し、2019 年以前のデータから将来の予測式を作成する。
2、作成された予測式を用いて将来の推計を行う。
この手順のイメージを 図 1 に示した。ここでは簡略化のため、GDP と労働需要という 2 つのデータについて、Input としての GDP が大きくなるほど、Output としての労働需要が大きくなるという関係を仮定した。まず図中 A では、2019 年までの実績値を用いた回帰分析(*1) により、GDP による労働需要の予測式を作成した。本来この予測式は数式であるが、図中では直線で表現している。次に図中 B では、予測式に将来の GDP 予想を代入することで将来の労働需要を得た。図のイメージで表現すれば、予測式(直線)と GDP 予想が交わる高さが将来の労働需要ということになる。
図 1: 予測式の作成と将来予測のイメージ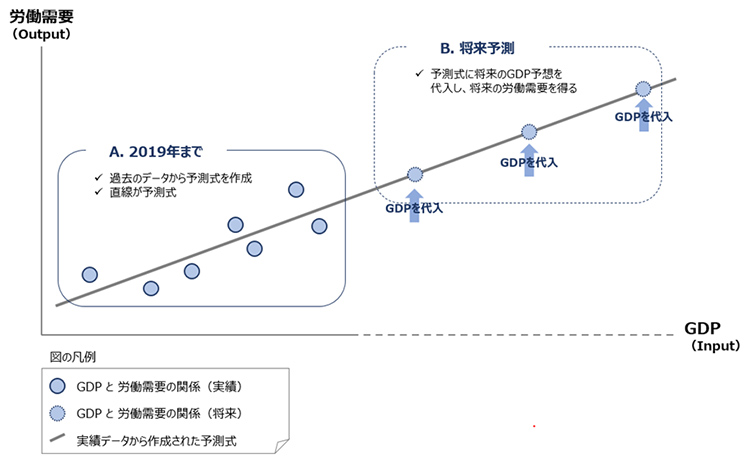
ここからは、各ブロックの詳細に移っていく。
需要ブロック
「需要ブロック」で推計するのは産業別就業者数の変化率である。得られた変化率を用いて、過去の就業者数から将来の必要就業者数を推計していく。需要ブロックの分析に用いた変数は産業別の生産額(名目 GDP)、賃金、労働時間、前年の就業者数である。なおここでの産業区分は 労働政策研究・研修機構 (2019) と同様であり、農林水産業、情報通信業、医療・福祉など、全部で 19 分類となっている。
産業別就業者数を推計する式は以下のとおり。![]()
式 1 の各変数について補足する。まず L は各産業における就業者数であり、ΔlnL(*2) は前年(t-1 年)から当年(t 年)への変化率を表している。次に、Z は以下のとおりである。
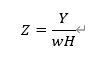
分子の Y は各産業における名目生産額(名目 GDP)、分母の w は時間当たり賃金、H は総労働時間である。つまり、一人当たりの賃金・労働時間に対する生産額の大きさが、必要な就業者数に影響を及ぼすことを意味している。最後に、const. は定数項、 εは誤差項であり(*3)、a, b, c はそれぞれ回帰分析の結果得られる係数である(*4)。
供給ブロック
「供給ブロック」で推計するのは、性・年齢階級別(女性は有配偶・無配偶別)の労働力率である。得られた労働力率を将来人口推計に乗じることによって、労働力人口を計算している。供給ブロックの分析に用いた変数は前期失業率や進学率などであり、性・年齢階級別に異なる。なお性・年齢階級の区分は 労働政策研究・研修機構 (2019) に従っている。
労働力率を推計する式は以下のとおり。
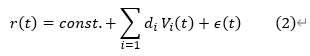
式 2 の各変数について補足する。まず r は各性・年齢階級における労働力率である(*5)。次に Vi は労働力率に影響を及ぼす政策や行動であり、具体例を以下に示す。
- 男性 20~24 歳では、労働力率に影響を及ぼす要因として「大学・短大進学率(2 期前)」「前期失業率」「当該年齢賃金/年齢計賃金」が分析に投入された。
- 女性 45~49 歳では、労働力率に影響を及ぼす要因として「前期失業率」「短時間雇用者比率」「実質賃金(賃金/CPI)」が分析に投入された。
- 女性 60~64 歳では、労働力率に影響を及ぼす要因として「前期失業率」「年金支給開始年齢(定額)」「コーホート要因(*6)」が分析に投入された。
最後に、di は回帰係数である。
需給調整ブロック
「需給調整ブロック」で推計するのは、有効求人倍率、賃金上昇率、失業率である。これらの値が間接的に労働需要、労働供給に影響を及ぼす。
まず、全年齢階級に共通の有効求人倍率を労働需給倍率(労働力需要/労働力人口)から求め、この値を年齢階級別の求人倍率に変換した。次に賃金上昇率は、有効求人倍率、消費者物価指数(CPI)の変化率、交易条件(輸出物価指数/輸入物価指数)から求めており、全年齢階級で共通である。最後に、失業率については各年齢階級の失業率から変換式を作成した。なお、将来の有効求人倍率は、2005 年から 2021 年の平均を外生的(*7)に与えている。
都道府県・職業別シミュレーション
都道府県・職業ごとの労働需給は、上記で得られた労働需給を国勢調査から作成した都道府県・職業の構成比(以下、構成比と表記)で按分して算出した(*8)。なお、労働需要については現在の構成比が固定であること、労働供給については構成比がトレンドをもって将来的に変化することを仮定した。
この構成比は、例えば農林水産業における北海道の事務職、輸送機械器具製造業における広島県の営業職といったように、ある産業に、その都道府県のその職業の人が何%いるかという値を示している。使用した国勢調査のデータは 2015 年と 2020 年のものである。労働需要については、内閣府発表の将来見通し(*9)をベースに、各産業における経済成長が概ね一定であると仮定したことを踏まえ、都道府県・職業の構成比も 2020 年で固定している。一方、労働供給については、労働環境や賃金、その他様々な条件で需要とは関連しない労働移動が発生する可能性を反映するため、都道府県・職業構成比の変化トレンドを作成し、適用した。構成比の変化トレンドは、都道府県・職業ごとに 2015 年から 2020 年までの平均変化率を求め、2040 年まで延長したものである。
解決策としての自動化とワーキッシュアクト
本プロジェクトでは労働供給制約という課題に対して、自動化とワーキッシュアクト(*10)(以降、WA と表記)という 2 つの中心的な解決策を想定した。それぞれ専門家や企業へのヒアリングを行ったほか、WA では働く人へのアンケート調査も実施し、実態把握を試みた。
得られた結果に対して研究所内で議論を行い、将来の自動化率、WA 参加率を算出し、労働供給を引き上げる要素としてモデルに組み込んだ。自動化と WA が需要ではなく供給側に組み込まれることについて、自動化ではロボットやテクノロジーが人と協働する未来、WA では従来型の労働ではない形で人々が社会参加する未来を想定している。まさに本プロジェクトが想定している「労働供給制約」に対し、従来の人による労働ではない労働を提供していくというものである。
おわりに
ここまでで、シミュレーションの概要について述べた。最後に、シミュレーションモデルの展望と結果を活用する上での考え方について 2 点触れたい。
第 1 に、シミュレーションは過去のデータから将来を予測する方法を取っているため、過去からの延長線上に未来を想定していることになる。また、予測式が過去のデータにうまく当てはまるほど、将来の変動に対する柔軟性が欠ける可能性もある。冒頭で述べたとおり、シミュレーションモデルは未来の「はたらく」を考えるための出発点である。行政、産業を含む様々な関係者を含む対話を通じ、より解像度高く「労働供給制約」の実態を捉えることで、未来の「はたらく」に対する有効な打ち手を検討することが望ましい。
第 2 に、都道府県や職業別の予測は国勢調査から得られたデータのみを反映している。例えば人が労働に参加するには、各都道府県、自治体独自の政策や文化からも影響を受けると考えられるが、このような影響は反映されていない。シミュレーション結果を各地域の政策や取組に活用する上では、独自の政策、文化、直近の状況など、数値だけでない情報も組み合わせて考えていく必要があるだろう。
上記のような課題を認識しつつも、今こそ考えたいのは、日本全体、あるいは各都道府県・自治体において自動化や WA、その他の様々な打ち手を講じることにより、将来このシミュレーションが「外れた」労働社会を作るよう努力することだと考える。
執筆(シミュレーション WG 担当):中村 星斗
(*1)ここでは、労働需要が GDP でどのように予測されるかの関係を明らかにする分析を示す。
(*2)Δ は「差」を意味する記号(デルタ)である。
(*3)定数項は名目 GDP や賃金などの変数によって変動しない部分を、誤差項は真の値と実際に得られた値の差を表す。供給ブロック、需給調整ブロックでも同様に登場する。
(*4)需要ブロックの例で言えば、名目 GDP や賃金などが就業者数の変化率に影響を及ぼす度合いを示している。図 1 では、予測式の傾きがこの回帰係数に該当する。
(*5)労働力率は分析結果が 100% を超えないよう、 R (%) を r=ln(R/(100-R)) によって変換した(ロジット変換)。
(*6)5 年前の 1 年齢階級若い労働力率を指す。例えば 2019 年における 60~64 歳のコーホート要因は、2014 年における 55~59 歳の労働力率である。
(*7)各シミュレーションモデル(方程式)の外側で決まる数値をモデルに代入すること。
(*8)都道府県単位ではない職業別のシミュレーションも考え方は同じであるため、ここでは都道府県・職業別の実施方法のみを記載している。
(*9)内閣府「中長期の経済財政に関する試算」(令和5年1月24日 経済財政諮問会議提出)
(*10)ワーキッシュアクト(Workish act)は、「何か社会に対して提供しているかもしれない、本業の仕事以外の活動」の総称。
引用文献
労働政策研究・研修機構. (2019). 労働力需給の推計 -労働力需給モデル(2018年度版)による将来推計 -. 独立行政法人 労働政策研究・研修機構.


 メールマガジン登録
メールマガジン登録 各種お問い合わせ
各種お問い合わせ

